
Do you want to know more about the solutions of quadratic equation by using formulae (plural of formula)? In this article, I’ll show you everything from start to end.
A quadratic equation is an expression of ax²+bx+c=o. The methods to use to solve quadratic equation are four (4) and they are listed below:
- Factorisation method
- Completing the square method
- Formula method and
- Graphic method.
But in this article today, I will show you how you will can solve a quadratic equation by factorisation method. Because the process of solving quadratic equation using factorisation method is a simplest one.
Read this also: how to calculate the cut-off mark mathematically to know whether you will be admitted or not.
Hence, let us start to teach you from the simplest one till we get to the simple or complex ones.
If we finish this post to an end, you will know how to solve factorisable quadratic equation by factorisation method.
Solving quadratic equation by factorisation method, you will deal with finding the sum and products of of the roots of the given equation.
You shouldn’t get worried about finding the sum and products of roots of the equation in quadratic question, because we will solve quadratic equation by using factorisation method right here in this article.
We will teach you how to solve quadratic equation by using the factorisation method today, and we will also show you all the needed explanations for you step-by-step.
Solving quadratic equation’s problem is easy especially when you use factorisation method.
How To Solve Quadratic Equation By Factorisation Method
Solution of quadratic equation by factorisation method.
The following examples explain how a quadratic equation can be solved using the factorisation method.
i. x²+7x+10=0
As we have suggested earlier, before you can solve any quadratic equation by factorisation method, you must find the sum of the middle and products of the constant terms in the equation.
By your physical assumption at this equation pointed above, the middle term of it is 7x and its constants are 10 qnd x². These then become 10x².
As you have been known the middle and constant terms in the equation as +7x and 10x² respectively, you would find two terms whose sum is +7x and product is 10x².
Therefore, x²+7x+10=0
Two terms whose sum is +7x and product is +10x² are 2x and 5x.
Hence, from the explanations given above, it is known that the sum of the middle and product of the constant terms are +2x and +5x respectively because, when you add 2 and 5, you will have an answer of 7 and if you multiply (product) 2 and 5 also, you will get 10.
Above are just the tips for showing you how to find the sum and product of middle and constant terms respectively of any the given quadratic equation when you are being asked to it by using the factorisation method.
Now, below are the couple of quadratic questions which we will solve in this article right now and right here.
Solutions And Examples Of Quadratic Equation By Factorisation Method
Below are the examples of quadratic equations and their solutions solved with factorization method. Examples are three (3) and they are:
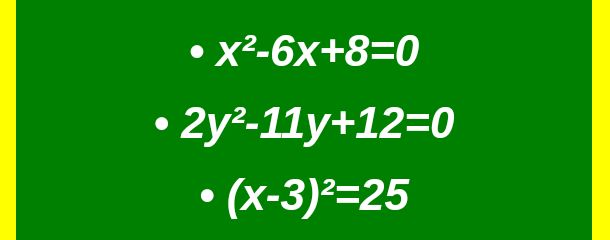
When I show you an answer of the question directly without solving, you may think I am a thief, right? Thus, any time we teach mathematics, we show the steps we took before getting a final answer.
1. x²-6x+8=0
Solution: sum of middle and product of constant terms= -6x and +8x² respectively.Then x²-6x+8=0 becomes x²-2x-4x+8=0.
Pairing: (x²-2x)-(4x+8)=0.
Factoring: x(x-2)-4(x-2)=0.
x-4=0, or x-2=0.
:. x=4, or x=2 (final answer)
2. 2y²-11y+12=0
Solution: middle and constant terms are 11y and 24y² respectively.Then equation 2y²-11y+12=0 becomes 2y²-3y-iy+12=0.
Pairing: (2y²-3y)-(8y+12)=0.
Factoring: y(2y-3)-4(2y-3)=0.
y-4=0, or 2y-3=0.
.: y=4, or y=3/2 (final answer)
3. (x-3)²=25
Solution:
opening the bracket= x²-6x+9=25.
x²-6x=25-9
x²-6x=16
x²-6x-16=0.
Sum of middle and product of constant terms are -6x and -16x² respectively and the term whose sum is -6x and product is -16x² are +2x and -8x.
Then the equation (x²-6x-16=0) becomes x²+2x-8x-16=0.
Pairing: (x²+2x)-(8x-16)=0.
Factoring: x(x+2)-8(x+2)=0
.: x-8=0, or x+2=0.
x=8, or x=-2.
Conclusion
Did you understand this article? Drop your comment in the comment box and remember to share it with your friends.
See also: Simultaneous Equations: Examples Of simultaneous Equation And Method For Solving It
If you know we’ve helped you know the solutions of quadratic equation by methods with examples, please share this article and also follow us on Facebook or Twitter for more Maths related posts.

